Just acoustic materials, no acoustic construction here (i.e., structural sound insulation). acoustic properties only, no internal properties of porous media.

Acoustic Material Properties

With the in-depth study and broad application of acoustic materials, the importance of the characterising acoustic material properties has emerged and risen gradually. The absorption properties and acoustic insulation properties are most used evaluation indexes for acoustic materials. The absorption properties include absorption coefficient and acoustic impedance; the acoustic insulation properties usually evaluated by the transmission losses.

Common acoustic material properties are——Absorption Coefficient， Acoustic Impedance Ratio，Transmission Loss.

Experimental Measurement

There are various methods used to measure and characterise acoustic materials.

Normal incidence (impedance or standing wave tube)

To understand and model absorptive materials better, it is necessary to measure materials in a more controlled environment to allow direct comparison between theory and experiment (numerical experiment included).

standing wave method

The steady state pressure in the tube is given by

p(z)=A\left(e^{jkz}+Re^{-jkz}\right) \tag{1}

Where $A$ is the a complex constant; $k$ is the wave number; R is the the reflection coefficient; $z$ is the relative position to the sample. The measurement of the minimum and maximum pressures of the standing wave is needed. The standing wave ratio $s$ is defined as the ratio of $p_{max}$ to $p_{min}$ and is given by:

s=\frac{p_{max}}{p_{min}} \tag{2}

The magnitude of the reflection coefficient and the absorption coefficient can be obtained:

|R|=\frac{s-1}{s+1} \tag{3}

\alpha{}=1-|R|^2 \tag{4}

One need to measure the distance between where the first minimum pressure appears and the surface of the material $x_1$ to obtain the acoustic impedance ratio $Z_s$ :

b=\frac{2x_1}{\lambda} \tag{5}

|\xi|^2=\frac{\left(2-\alpha\right)-2\sqrt{1-\alpha}\cos{2\pi{}b}}{\left(2-\alpha\right)+2\sqrt{1-\alpha}\cos{2\pi{}b}} \tag{6}

Z_s=\xi{}Z_0=\xi{}\rho_{0}c_0 \tag{7}

which $\lambda$ is the wave length of the single frequency wave.

transfer function method

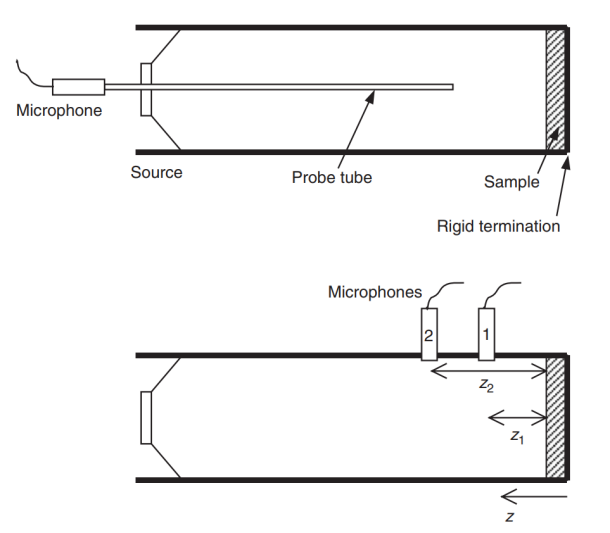
ImpedanceTube

Fig.1. Set-ups for impedance tube measurement (Source: Ref. 2)

The standing wave method can only test single frequency waves at a time and need longer tube to test lower frequency wave. By measuring the pressure at two points in the tube the transfer function method can set up and solve simultaneous equations for the reflection coefficient and from there get the impedance and absorption coefficient. This is the principle of the transfer function , often called the two-microphone method.

R=\frac{H_{12}e^{jkz_1}-e^{jkz_2}}{e^{-jkz_2}-H_{12}e^{-jkz_1}} \tag{8}

where, $H_{12}=p(z_2)/p(z_1)$

least mean square method

This method is essentially an adaptation of the transfer function method. It usually use three microphone to cover the frequency range an impedance tube offers.

Oblique incidence (semi-anechoic spaces)

For most practitioners, the only important measurement is that which gives the random incidence absorption coefficient that is needed for performance specifications in room designing, vegetation belt setting, and so on.

Reverberation room

The reverberation chamber test requires large sample sizes and a specialist test room, and so is expensive to undertake. It also only gives absorption coefficients; the impedance cannot be measured. Consequently, developers of absorptive material will often use the impedance tube to build up an understanding of the material properties on small samples, before undertaking reverberation tests.

The reverberation time of a room is dependent on the total absorption in the room. Consequently, by measuring the reverberation time of a room before and after a sample of absorbent is introduced, it is possible to calculate the random incidence absorption coefficient.

The reverberation time before the sample is introduced is given by:

T_0=\frac{55.3V}{c_0\alpha_0S+4Vm_1} \tag{9}

where $V$ is the room volume, $c_0$ is the speed of sound, $\alpha_0$ is the average absorption coefficient of the empty room, $S$ is the surface area of the room and $m_1$ is the air absorption constant.

The reverberation time after the sample is introduced is given by:

T_1=\frac{55.3V}{c_0\left(\alpha_0\left[S-S_s\right]+\alpha_sS_s\right)+4Vm_1} \tag{10}

where $S_s$ is the surface area and $\alpha_s$ is the absorption coefficient of the sample. By rearranging Equations $(9)$ and $(10)$ it is possible to obtain the absorption coefficient of the sample.

Reference

[1] Chen, ke , xiang . Zeng, and you . Yang. Sheng Xue Ce Liang. Bei jing: Ji xie gong ye chu ban she, 2010. Print.

[2] Cox, Trevor J., and Peter D’Antonio. Acoustic Absorbers and Diffusers: Theory, Design and Application. CRC Press, 2009.